| Codeforces Round 915 (Div. 2) |
|---|
| Finished |
You are given a tree$$$^{\dagger}$$$. In one zelda-operation you can do follows:
- Choose two vertices of the tree $$$u$$$ and $$$v$$$;
- Compress all the vertices on the path from $$$u$$$ to $$$v$$$ into one vertex. In other words, all the vertices on path from $$$u$$$ to $$$v$$$ will be erased from the tree, a new vertex $$$w$$$ will be created. Then every vertex $$$s$$$ that had an edge to some vertex on the path from $$$u$$$ to $$$v$$$ will have an edge to the vertex $$$w$$$.
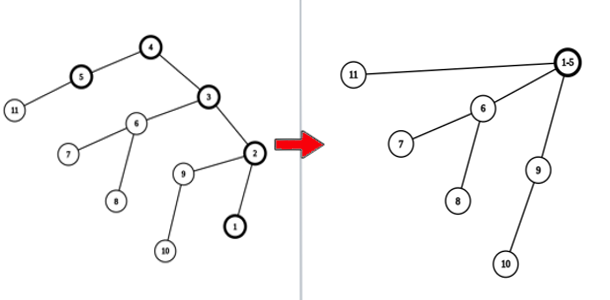 Illustration of a zelda-operation performed for vertices $$$1$$$ and $$$5$$$.
Illustration of a zelda-operation performed for vertices $$$1$$$ and $$$5$$$. Determine the minimum number of zelda-operations required for the tree to have only one vertex.
$$$^{\dagger}$$$A tree is a connected acyclic undirected graph.
Each test consists of multiple test cases. The first line contains a single integer $$$t$$$ ($$$1 \le t \le 10^4$$$) — the number of test cases. The description of the test cases follows.
The first line of each test case contains a single integer $$$n$$$ ($$$2 \le n \le 10^5$$$) — the number of vertices.
$$$i$$$-th of the next $$$n − 1$$$ lines contains two integers $$$u_i$$$ and $$$v_i$$$ ($$$1 \le u_i, v_i \le n, u_i \ne v_i$$$) — the numbers of vertices connected by the $$$i$$$-th edge.
It is guaranteed that the given edges form a tree.
It is guaranteed that the sum of $$$n$$$ over all test cases does not exceed $$$10^5$$$.
For each test case, output a single integer — the minimum number of zelda-operations required for the tree to have only one vertex.
441 21 33 493 13 53 25 66 77 87 96 471 21 32 44 53 62 761 21 31 44 52 6
1 3 2 2
In the first test case, it's enough to perform one zelda-operation for vertices $$$2$$$ and $$$4$$$.
In the second test case, we can perform the following zelda-operations:
- $$$u = 2, v = 1$$$. Let the resulting added vertex be labeled as $$$w = 10$$$;
- $$$u = 4, v = 9$$$. Let the resulting added vertex be labeled as $$$w = 11$$$;
- $$$u = 8, v = 10$$$. After this operation, the tree consists of a single vertex.
| Name |
|---|




