| Codeforces Round 932 (Div. 2) |
|---|
| Finished |
Master Andrey loves trees$$$^{\dagger}$$$ very much, so he has a tree consisting of $$$n$$$ vertices.
But it's not that simple. Master Timofey decided to steal one vertex from the tree. If Timofey stole vertex $$$v$$$ from the tree, then vertex $$$v$$$ and all edges with one end at vertex $$$v$$$ are removed from the tree, while the numbers of other vertices remain unchanged. To prevent Andrey from getting upset, Timofey decided to make the resulting graph a tree again. To do this, he can add edges between any vertices $$$a$$$ and $$$b$$$, but when adding such an edge, he must pay $$$|a - b|$$$ coins to the Master's Assistance Center.
Note that the resulting tree does not contain vertex $$$v$$$.
Timofey has not yet decided which vertex $$$v$$$ he will remove from the tree, so he wants to know for each vertex $$$1 \leq v \leq n$$$, the minimum number of coins needed to be spent to make the graph a tree again after removing vertex $$$v$$$, as well as which edges need to be added.
$$$^{\dagger}$$$A tree is an undirected connected graph without cycles.
Each test consists of multiple test cases. The first line contains a single integer $$$t$$$ ($$$1 \le t \le 10^4$$$) — the number of test cases. The description of the test cases follows.
The first line of each test case contains a single integer $$$n$$$ ($$$5 \le n \le 2\cdot10^5$$$) — the number of vertices in Andrey's tree.
The next $$$n - 1$$$ lines contain a description of the tree's edges. The $$$i$$$-th of these lines contains two integers $$$u_i$$$ and $$$v_i$$$ ($$$1 \le u_i, v_i \le n$$$) — the numbers of vertices connected by the $$$i$$$-th edge.
It is guaranteed that the given edges form a tree.
It is guaranteed that the sum of $$$n$$$ over all test cases does not exceed $$$2\cdot10^5$$$.
For each test case, output the answer in the following format:
For each vertex $$$v$$$ (in the order from $$$1$$$ to $$$n$$$), in the first line output two integers $$$w$$$ and $$$m$$$ — the minimum number of coins that need to be spent to make the graph a tree again after removing vertex $$$v$$$, and the number of added edges.
Then output $$$m$$$ lines, each containing two integers $$$a$$$ and $$$b$$$ ($$$1 \le a, b \le n, a \ne v, b \ne v$$$, $$$a \ne b$$$) — the ends of the added edge.
If there are multiple ways to add edges, you can output any solution with the minimum cost.
351 31 44 53 254 24 33 55 152 11 51 41 3
1 1 3 4 0 0 1 1 1 2 2 1 3 5 0 0 0 0 0 0 1 1 1 2 1 1 1 2 1 1 1 2 3 3 2 3 4 5 3 4 0 0 0 0 0 0 0 0
In the first test case:
Consider the removal of vertex $$$4$$$:
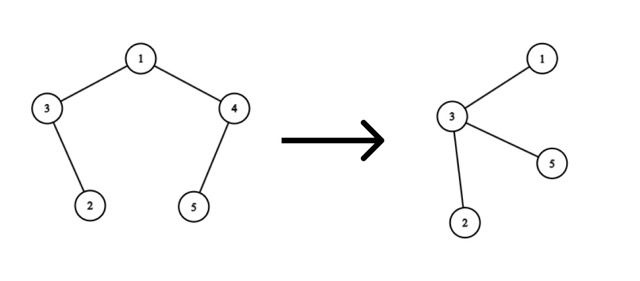
The optimal solution would be to add an edge from vertex $$$5$$$ to vertex $$$3$$$. Then we will spend $$$|5 - 3| = 2$$$ coins.
In the third test case:
Consider the removal of vertex $$$1$$$:
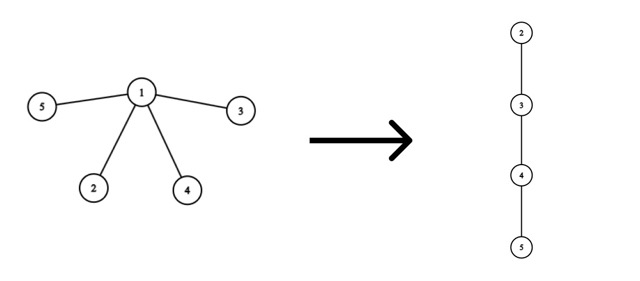
The optimal solution would be:
- Add an edge from vertex $$$2$$$ to vertex $$$3$$$, spending $$$|2 - 3| = 1$$$ coin.
- Add an edge from vertex $$$3$$$ to vertex $$$4$$$, spending $$$|3 - 4| = 1$$$ coin.
- Add an edge from vertex $$$4$$$ to vertex $$$5$$$, spending $$$|4 - 5| = 1$$$ coin.
Then we will spend a total of $$$1 + 1 + 1 = 3$$$ coins.
Consider the removal of vertex $$$2$$$:
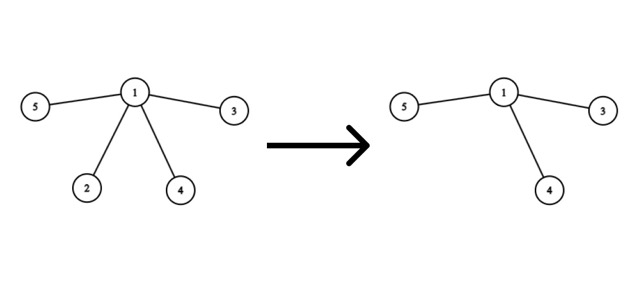
No edges need to be added, as the graph will remain a tree after removing the vertex.
| Name |
|---|




