| Codeforces Round 936 (Div. 2) |
|---|
| Finished |
You are given a tree with $$$n$$$ vertices.
Your task is to find the maximum number $$$x$$$ such that it is possible to remove exactly $$$k$$$ edges from this tree in such a way that the size of each remaining connected component$$$^{\dagger}$$$ is at least $$$x$$$.
$$$^{\dagger}$$$ Two vertices $$$v$$$ and $$$u$$$ are in the same connected component if there exists a sequence of numbers $$$t_1, t_2, \ldots, t_k$$$ of arbitrary length $$$k$$$, such that $$$t_1 = v$$$, $$$t_k = u$$$, and for each $$$i$$$ from $$$1$$$ to $$$k - 1$$$, vertices $$$t_i$$$ and $$$t_{i+1}$$$ are connected by an edge.
Each test consists of several sets of input data. The first line contains a single integer $$$t$$$ ($$$1 \le t \le 10^4$$$) — the number of sets of input data. This is followed by a description of the sets of input data.
The first line of each set of input data contains two integers $$$n$$$ and $$$k$$$ ($$$1 \le k < n \le 10^5$$$) — the number of vertices in the tree and the number of edges to be removed.
Each of the next $$$n - 1$$$ lines of each set of input data contains two integers $$$v$$$ and $$$u$$$ ($$$1 \le v, u \le n$$$) — the next edge of the tree.
It is guaranteed that the sum of the values of $$$n$$$ for all sets of input data does not exceed $$$10^5$$$.
For each set of input data, output a single line containing the maximum number $$$x$$$ such that it is possible to remove exactly $$$k$$$ edges from the tree in such a way that the size of each remaining connected component is at least $$$x$$$.
65 11 21 33 43 52 11 26 11 22 33 44 55 63 11 21 38 21 21 32 42 53 63 73 86 21 22 31 44 55 6
2 1 3 1 1 2
The tree in the first set of input data:
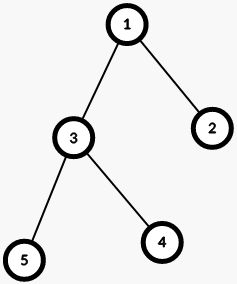
After removing the edge $$$1$$$ — $$$3$$$, the tree will look as follows:
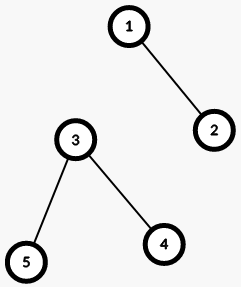
The tree has split into two connected components. The first component consists of two vertices: $$$1$$$ and $$$2$$$. The second connected component consists of three vertices: $$$3, 4$$$ and $$$5$$$. In both connected components, there are at least two vertices. It can be shown that the answer $$$3$$$ is not achievable, so the answer is $$$2$$$.
| Name |
|---|




