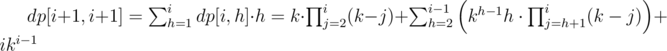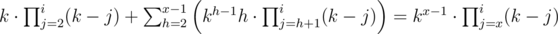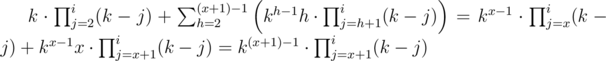Постановка задачи:

Имеется n деталей и два станка. Каждая деталь должна сначала пройти обработку на первом станке, затем — на втором. При этом i-ая деталь обрабатывается на первом станке за a_i времени, а на втором — за b_i времени. Каждый станок в каждый момент времени может работать только с одной деталью.

Требуется составить такой порядок подачи деталей на станки, чтобы итоговое время обработки всех деталей было бы минимальным.

Решение задачи описано на e-maxx.ru

Перед дальнейшим чтением рекомендую ознакомиться с приведенным там решением, здесь будут обсуждены некоторые его проблемы.

Опуская доказательства: в решении предлагается отсортировать пары чисел (a_i, b_i) следующим компаратором: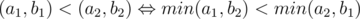

Мы определили некоторое бинарное отношение на множестве пар чисел. Внимание, вопрос: почему этим отношением можно пользоваться как компаратором?

Сначала о плюсах: Это отношение действительно транзитивно.

Давайте это докажем (если вы хотите минусов, эту часть можно пропустить).

Дано: min(a₁, b₂) < min(a₂, b₁), min(a₂, b₃) < min(a₃, b₂).

Доказать: min(a₁, b₃) < min(a₃, b₁)

Доказательство: от противного. Предположим min(a₁, b₃) ≥ min(a₃, b₁)

Есть два варианта:

1) a₁ ≤ b₂

Из этого следует a₁ < a₂, a₁ < b₁. Из нашего предположения получаем, что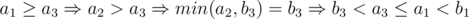

Отсюда min(a₁, b₃) ≤ b₃ < min(a₃, b₁)

2) a₁ > b₂

Из этого следует b₂ < a₂, b₂ < b₁.

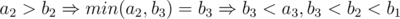
Отсюда min(a₁, b₃) ≤ b₃ < min(a₃, b₁)

Получили противоречие.

Ч.т.д.

А вот теперь о минусах. Очевидно, это отношение не обладает свойством антисимметричности. Более того: Давайте на множестве пар чисел введем отношение "быть равными" в том смысле, что ни одна из пар не больше другой. 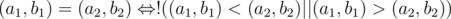. Это отношение транзитивным не является!

Пример: (2, 3) = (1, 1) = (4, 5), но (2, 3) < (4, 5).

Справедливости ради: Можно показать, что если (a₁, b₁) = (a₂, b₂) = (a₃, b₃) и a₂! = b₂, то (a₁, b₁) = (a₃, b₃)

Давайте определим отсортированную последовательность так: Последовательность отсортирована по неубыванию, если для любых 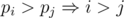, т.е. никогда больший элемент не идет перед меньшим.

Построим ориентированный граф так: Вершины — элементы последовательности, дуга из i в j соответствует p_i < p_j. Тогда наше определение отсортированной последовательности совпадает с топологической сортировкой этого графа.

Мы показали, что ориентированных циклов в этом графе нет, а значит на нем есть топологическая сортировка, т.е. нашу последовательность можно отсортировать.

Но если мы просто передадим наш компаратор в пузырьковую сортировку, то последовательность не будет отсортирована.

Пример: (4, 5), (1, 1), (2, 3)

Думаю, что для остальных сортировок тоже несложно будет подобрать соответствующий пример (возможно, он будет зависеть от конкретной реализации, потому что все такие контрпримеры завязаны на обработке "равных" элементов).

Таким образом, доказательство на e-maxx не верно.

Кто готов поделиться своими красивыми решениями?

Тема такая: У меня завтра ДР, и мы собираемся отпраздновать прекрасным контестом в какой-нибудь уютной кафешечке.
И мы даже готовы писать серьезную тренировку, но все же пытались найти какой-нибудь веселый праздничный контест.
Соответственно, возник такой вопрос: существуют ли они где-нибудь в природе, праздничные контесты?)
Например, контесты с серьезными задачами, но тематическими уральскими графоманскими сказочками предысториями?
Всем заранее спасибо)

Вступление

Задача меня порадовала (часть про [1...k], разумеется), на самом контесте я написал двухмерную динамику 3458123, но ограничения позволяли написать что угодно :)

Слышал я о решении полным перебором за k^k + 2. Но после контеста я узнал о волшебной формуле ans = k^k - 1

Поначалу не верилось, что это так. Но потом лень была побеждена, я взял тетрадку и ручку и начал считать свою динамику. Формула была выведена, но не очень-то быстро и красиво.

А теперь о причине, побудившей меня написать это: лично я понятия не имел (и не имею) о том, что такое Cayley trees. Поэтому хочу постараться подробно описать вывод формулы, не требующий никаких знаний.

Надеюсь, вы найдете у меня ошибку ;)

Динамика

Начнем с попытки прогенерировать первые номера домов.

Номер первого дома может быть любым от 1 до k, т.к. нам все равно придется искать путь из дома с этим номером в первый.

Условно обозначим это 1... (потом станет понятнее, почему обозначение именно такое), соответствующих вариантов у нас k.

Для номера второго дома есть три принципиально различных варианта:

1. 1. усл.об. — 11..., вариантов — k*1=k
2. 1. Но тогда мы не сможем попасть к первому дому от второго.

3. 3 и более. Кол-во вариантов — k*(k-2). усл.об. — 13... Почему именно 3 ? Потому что если не 3, то мы вполне можем поменять местами дома так, чтобы этот стал третьим.

Переходим к третьему дому от первого варианта:

1. 1 или 2. вариантов — k*2=2k. усл.об. — 111... Вот тут важный момент. Почему 112 не отличается от 111 ? Потому что и так, и так мы сможем дойти от всех домов к первому. Таким образом, '1' в усл.об. характеризует то, что от данного дома мы уже можем добраться до первого, а значит теперь необязательно стремиться в первый дом, можно стремиться в один из них.

... (дальше понятно)

Тогда посчитаем такую двухмерную динамику: в dp[x,y] будем хранить кол-во вариантов таких, что "обработано" уже х домов, причем из первых y из них мы можем попасть в первый. Из попыток генерации вполне понятно, как пересчитывать:

dp[1,1]=k

(j<i) dp[i, j] = dp[i - 1, j]·(k - i)

Ответом, очевидно, будет являться dp[k,k]

Вывод формулы

Путем анализа формул пересчета и божественного рандома заметим

(i>1) dp[i, i] = k^i - 1

(1<j<i)

Теперь докажем эти формулы по индукции.

База индукции dp[1,1]=k верна.

(j<=i)

Для доказательства докажем индукцией по х такое равенство:

База индукции х=2, очевидно, верна.

Подставляя в полученное равенство x=i, получаем

dp[i + 1, i + 1] = k^i - 1(k - i) + k^i - 1i = k^{(i + 1) - 1}

Таким образом, формулы доказаны, а значит dp[k, k] = k^k - 1 для всех k>1

Но так уж получилось, что 1 = 1^0, поэтому можно считать ответ всегда равным k^k - 1