Корневое дерево называется хорошим, если каждая вершина дерева либо является листом (вершиной без детей), либо имеет ровно $$$m$$$ детей.
Пусть на хорошем дереве на каждом листе $$$u$$$ записано положительное целое число $$$c_{u}$$$. Мы определяем значение листа как $$$c_{u} + \mathrm{dep}_{u}$$$, где $$$\mathrm{dep}_{u}$$$ — количество ребер на пути от вершины $$$u$$$ до корня (также известное как глубина $$$u$$$). Ценность хорошего дерева — это максимальное значение всех его листьев.
Вам дан массив из $$$n$$$ целых чисел $$$a_{1}, a_{2}, \ldots, a_{n}$$$, которые должны быть записаны на листьях. Вам нужно построить хорошее дерево из $$$n$$$ листьев и записать целые числа из массива $$$a$$$ во все листья. Формально, вы должны выбрать для каждого листа $$$u$$$ индекс $$$b_{u}$$$, где $$$b$$$ — перестановка длины $$$n$$$, означающая, что целое число, записанное на листе $$$u$$$, равно $$$c_u = a_{b_{u}}$$$. При этих ограничениях вам необходимо минимизировать ценность хорошего дерева.
У вас есть $$$q$$$ запросов. Каждый запрос задается парой целых чисел $$$x$$$ и $$$y$$$ и меняет $$$a_{x}$$$ на $$$y$$$, после чего вы должны вывести минимальное значение хорошего дерева для заданного массива $$$a$$$.
Перестановкой длины $$$n$$$ называется массив, состоящий из $$$n$$$ различных целых чисел от $$$1$$$ до $$$n$$$ в произвольном порядке. Например, $$$[2,3,1,5,4]$$$ — это перестановка, но $$$[1,2,2]$$$ не является перестановкой ($$$2$$$ встречается в массиве дважды), также как и $$$[1,3,4]$$$ не является перестановкой ($$$n=3$$$, но в массиве есть элемент равный $$$4$$$).
Каждый тест содержит несколько наборов входных данных. Первая строка содержит единственное целое число $$$t$$$ ($$$1 \le t \le 10^4$$$) — количество наборов входных данных. Далее следует описание наборов входных данных.
Первая строка содержит три целых числа $$$n$$$, $$$m$$$ и $$$q$$$ ($$$1\le n,q \le 2 \cdot 10^5$$$, $$$2\le m \le 2\cdot 10^5$$$, $$$n \equiv 1 \pmod {m - 1}$$$) — количество листьев, константа $$$m$$$ и количество запросов.
Вторая строка содержит $$$n$$$ целых чисел $$$a_{1},a_{2}, \ldots, a_{n}$$$ ($$$1 \le a_{i} \le n$$$) — исходный массив.
В следующих $$$q$$$ строках описываются запросы изменения. Каждая строка содержит два целых числа $$$x$$$ и $$$y$$$ ($$$1\le x,y\le n$$$), представляющих запрос, изменяющий $$$a_{x}$$$ на $$$y$$$.
Гарантируется, что сумма $$$n$$$ и сумма $$$q$$$ не превосходят $$$2\cdot 10^5$$$.
Для каждого набора входных данных выведите $$$q$$$ целых чисел, $$$i$$$-е из которых — минимальная ценность дерева после $$$i$$$-го изменения.
35 3 33 3 4 4 51 42 43 55 2 43 3 4 4 51 42 53 54 57 3 41 2 2 3 3 3 41 42 15 56 6
6 6 6 7 7 7 8 6 6 6 7
В первом наборе входных данных после первого запроса текущий массив $$$a$$$ равен $$$[4,3,4,4,5]$$$. Мы можем построить такое хорошее дерево:
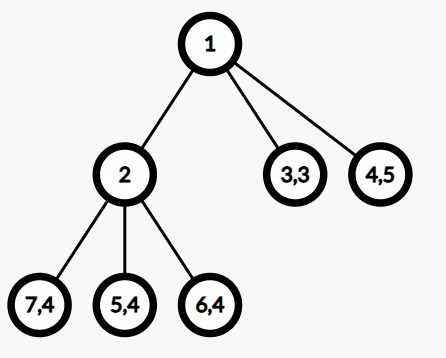
Первое число внутри вершины — это ее номер (в этой задаче номер вершины не имеет значения, но помогает понять рисунок). Если вершина является листом, то второе число внутри вершины — это число, написанное на ней.
Заметим, что $$$\mathrm{dep}_{3}=\mathrm{dep}_{4}=1,\mathrm{dep}_{5}=\mathrm{dep}_{6}=\mathrm{dep}_{7}=2$$$, и ценность дерева, которая является максимальным значением по всем листьям, равна $$$5+1=6$$$. Значения листьев $$$5$$$, $$$6$$$ и $$$7$$$ также равны $$$6$$$. Можно показать, что это дерево имеет минимальную ценность среди всех допустимых деревьев.
| Название |
|---|




