| Codeforces Round 933 (Div. 3) |
|---|
| Закончено |
Бернарду не помогло строительство мостов, и он все равно продолжил везде опаздывать. Тогда Рудольф решил научить его оптимально пользоваться метро.
Рудольф изобразил карту метро как неориентированный связный граф, не имеющий петель, в котором вершины представляют собой станции метро. Любая пара вершин соединяется не более чем одним ребром.
Две вершины соединяются ребром, если между соответствующими станциями метро можно переместиться на поезде напрямую, минуя другие станции. Метро в городе, в котором живут Рудольф и Бернард, имеет цветовую нотацию. Это значит, что любое ребро между какими-либо станциями имеет определенный цвет. Ребра определенного цвета в совокупности образуют ветку метро. Ветка метро не может содержать не связанные между собой ребра, то есть образует связный подграф заданного графа метро.
Пример карты метро приведен на рисунке.
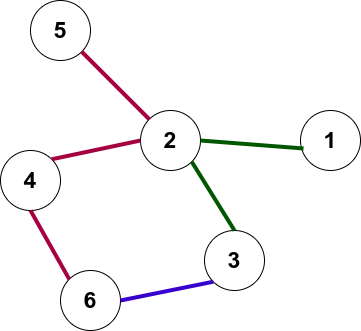
Рудольф утверждает, что маршрут будет максимально оптимальным, если он будет проходить через минимальное количество веток.
Помогите Бернарду определить это минимальное количество для заданных станций отправления и назначения.
Первая строка содержит одно целое число $$$t$$$ ($$$1 \le t \le 10^4$$$) — количество наборов входных данных.
Далее следуют описания наборов.
Первая строка набора содержит целые числа $$$n$$$ и $$$m$$$ ($$$2 \le n \le 2 \cdot 10^5, 1 \le m \le 2 \cdot 10^5$$$) — количество станций метро и количество прямых маршрутов между станциями (то есть ребер графа).
Далее следует $$$m$$$ строк — описание ребер. Каждая строка описания содержит три целых числа $$$u$$$, $$$v$$$ и $$$c$$$ ($$$1 \le u, v \le n, u \ne v, 1 \le c \le 2 \cdot 10^5$$$) — номера вершин, между которыми есть ребро, и цвет этого ребра. Гарантируется, что ребра одного цвета образуют связный подграф заданного графа метро. Между каждой парой вершин не более одного ребра.
Далее следует два целых числа $$$b$$$ и $$$e$$$ ($$$1 \le b, e \le n$$$) — станции отправления и назначения.
Сумма всех $$$n$$$ по всем наборам входных данных не превосходит $$$2 \cdot 10^5$$$. Аналогично, сумма всех $$$m$$$ по всем наборам входных данных не превосходит $$$2 \cdot 10^5$$$.
Для каждого набора входных данных выведите единственное целое число — минимальное количество веток, через которое может пройти маршрут от станции $$$b$$$ до станции $$$e$$$.
56 61 2 12 3 15 2 22 4 24 6 23 6 31 36 61 2 12 3 15 2 22 4 24 6 23 6 31 66 61 2 12 3 15 2 22 4 24 6 23 6 36 64 31 2 11 3 14 1 12 36 71 2 431 3 344 6 436 3 432 3 435 3 434 5 431 6
1 2 0 1 1
37 92 4 13 6 12 3 51 7 14 7 12 5 45 4 43 4 13 7 15 36 56 5 836914 1 836915 4 836913 2 836914 3 836915 16 76 1 836916 2 836912 5 836915 6 836912 3 836915 4 835743 5 836911 4
2 1 2
Граф метро для первого примера приведен на рисунке в условии.
В первом наборе тестовых данных из вершины $$$1$$$ в вершину $$$3$$$ можно добраться по пути $$$1 \rightarrow 2 \rightarrow 3$$$, воспользовавшись только зеленой веткой.
Во втором наборе тестовых данных из вершины $$$1$$$ в вершину $$$6$$$ можно добраться по пути $$$1 \rightarrow 2 \rightarrow 3 \rightarrow 6$$$, воспользовавшись зеленой и синей веткой.
В третьем наборе тестовых данных из вершины $$$6$$$ в ту же самую вершину не нужно ехать, поэтому количество веток равно $$$0$$$.
В четвертом наборе тестовых данных все ребра графа принадлежат одной ветке, поэтому ответ $$$1$$$.
| Название |
|---|




