This is the problem statement:
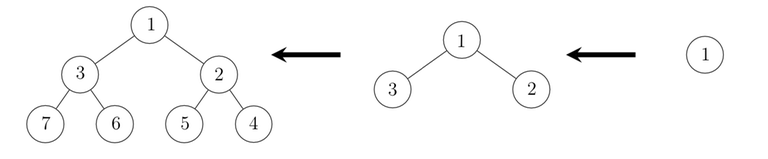
Bob decided to draw a binary tree. At the first step he draws a node and writes the number $$$1$$$ in it. At each step after this for any vertex that has a degree of 0 or 1 he does this: let the number in that vertex be $$$x$$$. Bob will draw two new vertices, draw and edge from each of them to this one and write the number $$$2x$$$ in one and $$$2x + 1$$$ in the other. below you can see a picture of the tree after 1, 2 and 3 steps.
Let the value of a graph be the bitwise AND of the numbers written on it's vertices and let $$$f(n)$$$ be the sum of the values of all conected subgraphs of the tree after $$$n$$$ steps. For example $$$f(1) = 1$$$ and $$$f(2) = 7$$$. Now answer these questions: (1) Find the value of $$$f(4)^3 \mod{\Delta}$$$. (2) Find the value $$$f(16) \mod{\Delta}$$$. (3) Find the value of $$$f(64) \mod{\Delta}$$$. Where $$$\Delta = 229939$$$.
I solved the first two parts like this: lets count the number conected subgraphs such that in the binary representation of their value the $$$i$$$th digit is $$$1$$$ for every $$$0 \leq i < n$$$ and then using this we can easily calculate the answer. But how do we find this number for a fixed $$$i$$$? we will run a DFS on the tree and visit only the nodes such that in the binary representation of the value written in them the $$$i$$$th digit is $$$1$$$. Then if we let $$$\textrm{sub}(v)$$$ be the number of such conected subgraphs roted at $$$v$$$ ($$$v$$$ is the number written on the vertex) then we have the recursive formula $$$\textrm{sub}(v) = (\textrm{sub}(2v) + 1)(\textrm{sub}(2v + 1) + 1)$$$. as you can see this algorithm works in $$$O(n\cdot2^n)$$$ wich is too slow for the third part of the problem. So for the third part I tried counting the number of conected subgraphs directly and without using a DFS but I couldn't get a formula for it. I would be thankful if you could give me a solution or a hint for the third part.