I realized that the previous post doesn't exactly explain how to actually work out the solutions to the Sprague-Grundy problems, or how to code them. Within this follow-up blog, I shall attempt to explain some of my thought process on working through Sprague-Grundy and similar problems, as well as including some code.
First, some pseudo-code of calculating the Sprague-Grundy, and how to find the MEX.
However, this implementation is inefficient, as it's not memoized, and we might recompute Sprague-Grundy of certain games quite a lot. Usually, if the game is just in terms of stack size, we can just go in increasing order to evaluate, since each move reduces the stack size, and we would have stored the values for smaller stacks into an array.
Consider a game where we're given a set S of numbers by which we can reduce the size of a pile. The following outlines how to use an array to calculate the Sprague-Grundy of a single pile.
Now, since we've computed the Sprague-Grundy for any given pile, we can determine who wins given a list of piles in the starting position in linear time. The S-Nim problem on kattis is basically these.
Now, for solutions, or outlines of such, to the problems from the previous blog:



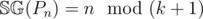 . This can be proven by strong induction.
. This can be proven by strong induction.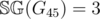 ,
,  .
. 


